Ellipse
Ellipses
are of fundamental importance in the history of science and physics. They were already well known and studied in antiquity, but became particularly important in the context of planetary motion (Kepler's 1st law) alias as solutions to the two-body problem of Newton's theory of gravity. Here, I present two not-so-familiar geometric constructions of an ellipse. The left one plays a particularly important role in Feynman's famous "Lost Lecture."
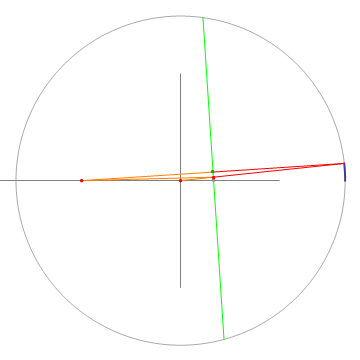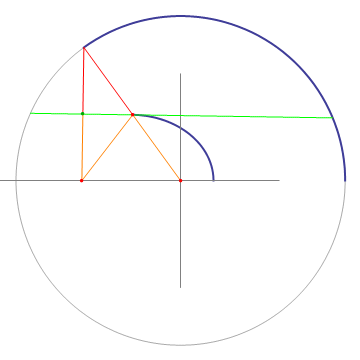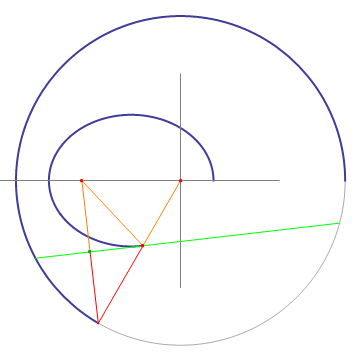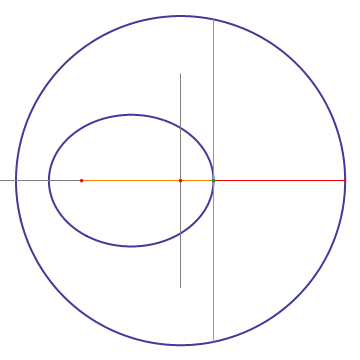
Take a circle and one off-center point. For a given point on the circle, draw a line to the circle's center and to the off-center point. Draw the bisectrix (green) to the line from the point on the circle to the off-center point, and find the intersection of this bisectrix with the line from the point on the circle to the circle center. This intersection will draw an ellipse when the point on the circle moves around. The proof is obvious when realizing that the orange lines are mirror images of the red lines mirrored on the bisectrix.
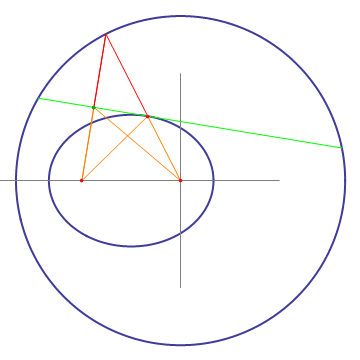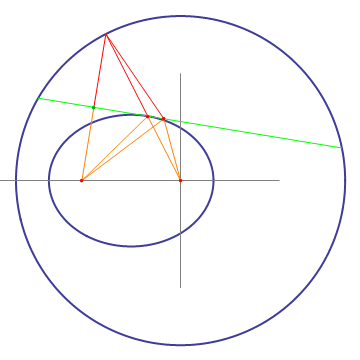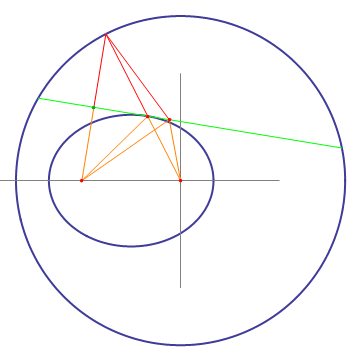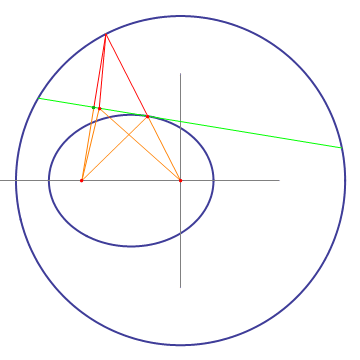
An important property of the left construction is that the bisectrix (green) is tangent to the ellipse. This can be seen by moving a point along the bisectrix. Only when the point touches the ellipse, the sum of the distances from it to the ellipse's foci is minimal, so all other points on the bisectrix have to be outside of the ellipse. Another interesting property which can be gleaned from the animation is that light starting from one focus of the ellipse will be reflected by the ellipse into the other focus.

Another interesting way to construct an ellipse: Draw all points for which the ratio of the distance from a fixed point (red) to the distance from a line (green) is a constant c. If this ratio c
is smaller than one, the curve is closed and forms an ellipse (as shown here). Proof: Let the distance between the fixed point and the line be d. In Cartesian coordinates centered at the fixed point, we have (x2
+ y2)1/2
= c·(d
- x). Taking the square of both sides, we find a quadratic form in x
and y, which describes indeed an ellipse for c
< 1. For c
= 1, we obtain a parabola, and for a c
> 1, a hyperbola.